Korelasi Pearson, Korelasi Kendall, Korelasi Spearman dan Cara Perhitungannya

PENUGASAN MATA KULIAH STATISTIK

Nama : Ria Suci Nurhalizah

NIM : 210112004

Prodi/smt : S1 Sistem Informasi/2

KORELASI PEARSON

Korelasi Pearson adalah alat analisis statistik yang digunakan untuk melihat keeratan hubungan linier antara 2 variabel yang skala datanya adalah interval atau rasio.

Ukuran korelasi ρ linear diantara dua variabel x (independen) dan y (dependend) diduga dengan sampel koefisien korelasi r yang dirumuskan sebagai berikut:

$r=\frac{n\sum_{i=1}^{n}X_{i}Y_{i}-\sum_{i=1}^{n}X_{i}\sum_{i=1}^{n}Y_{i}}{\sqrt{(n\sum_{i=1}^{n}X_{i}^{2}-(\sum_{i=1}^{n}X_{i})^{2})(n\sum_{i=1}^{n}Y_{i}^{2}-(\sum_{i=1}^{n}Y_{i})^{2})}}$

Di mana:

rxy: koefisien korelasi r pearson
n: jumlah sampel/observasi
x: variabel bebas/variabel pertama
y: variabel terikat/variabel kedua.

Dasarnya dalam korelasi Pearson Product Moment hanya digunakan untuk 2 variabel saja. Jika lebih dari dua variabel maka dapat digunakan dengan menggunakan korelasi berganda atau dengan menggunakan pendekatan analisis ragam.

Ditinjau dari segi arah korelasi :

Apabila hasil koefisien korelasi bernilai positif maka memiliki dua arti. Yaitu:

Apabila nilai variabel ditingkatkan, maka akan meningkatkan nilai variabel yang lain
Apabila nilai variabel diturunkan, maka akan menurunkan nilai variabel yang lain

Apabila hasil koefisien korelasi bernilai negatif maka memiliki dua arti pula. Yaitu:

Apabila nilai variabel ditingkatkan, maka akan menurunkan nilai variabel yang lain
Apabila nilai variabel diturunkan, maka akan meningkatkan nilai variabel yang lain

Ditinjau dari segi kekuatan korelasi, dilihat dari interval koefisien korelasi berada. Apabila hasil nilai absolut (mutlak) koefisien korelasinya adalah 0 maka tidak ada hubungan. Namun apabila hasil absolut koefisien korelasinya adalah 1 maka hubungannya sempurna.

Pengujian lanjutan untuk menentukan apakah koefisien korelasi yang didapat bisa digunakan untuk generalisasi atau mewakili populasi, maka digunakan uji signifikansi dari uji t. Maka nilai r pearson yang didapat digunakan untuk menghitung nilai t hitung. Berikut rumusnya:

Nilai t hitung yang di dapat nantinya kita bandingkan dengan nilai t tabel. Apabila t hitung > t tabel pada derajat kepercayaan tertentu, misal 95 % maka berarti signifikan atau bermakna.

Contoh Soal
Berikut ini merupakan data perusahaan mengenai harga permintaan suatu komoditi (X) dan harga rata-rata suatu komoditi (Y) disajikan dalam tabel berikut:

X	Y
178	105
224	105
160	130
315	130
229	130
250	150
181	150
306	170
257	170
300	180

Hitunglah koefisien korelasi pada kasus tersebut dan bagaimana arti dari hasil koefisien korelasi yang didapat!

Jawaban
Berikut ini hasil perhitungan tabel untuk mendapatkan nilai total untuk X, Y, X², Y², dan XY:

Data	X	Y	X²	Y²	XY
1	178	105	31684	11025	18690
2	224	105	50176	11025	23520
3	160	130	25600	16900	20800
4	315	130	99225	16900	40950
5	229	130	52441	16900	29770
6	250	150	62500	22500	37500
7	181	150	32761	22500	27150
8	306	170	93636	28900	52020
9	257	170	66049	28900	43690
10	300	180	90000	32400	54000
Total	2400	1420	604072	207950	348090

Dengan memasukan nilai total dari semua variabel pada tabel dan jumlah data ke dalam rumus korelasi Pearson Product Moment maka didapat hasil sebagai berikut:

$r=\frac{n\sum_{i=1}^{n}X_{i}Y_{i}-\sum_{i=1}^{n}X_{i}\sum_{i=1}^{n}Y_{i}}{\sqrt{(n\sum_{i=1}^{n}X_{i}^{2}-(\sum_{i=1}^{n}X_{i})^{2})(n\sum_{i=1}^{n}Y_{i}^{2}-(\sum_{i=1}^{n}Y_{i})^{2})}}$
$r=\frac{10(348090)-(2400)(1420)}{\sqrt{(10(604072)-(2400)^{2})(10(207950)-(1420)^{2})}}$
$r=0.5477$

Maka nilai koefisien korelasi Pearson Product Momentnya adalah 0.5477.

KORELASI KENDALL

Korelasi Kendall Tau statistik nonparametrik dengan skala pengukuran data sekurang-kurangnya data ordinal. Korelasi kendall tau digunakan untuk mengukur tingkat kesesuaian yakni apakah ada perbedaan tingkat kesesuain ranking antara 2 variabel yang diamati.

rumus yang bisa digunakan, yaitu:

τ = S 1 2 n ( n - 1 )

S merupakan skor keseluruhan atau grand total. Umumnya, skor tersebut adalah jumlah dari skor urutan kewajaran yang berasal dari pasangan data pada salah satu variable yang digunakan.Dalam uji ini, jika urutan ranking termasuk wajar, maka akan diberikan skor +1. Namun, apabila urutan ranking tersebut tidak wajar, maka akan diberikan nilai -1. N sendiri dalam rumus tersebut adalah banyaknya pasangan ranking yang menjadi objek dalam pengujian.

Contoh Soal

Dalam salah satu kasus, terdapat tabel:

Observasi	Ranking
Observasi	X	Y
A	3	3
B	4	1
C	2	4
D	1	2

Kemudian, pada variable X diurutkan sehingga variabel Y mengikuti. Tabel tersebut berubah menjadi:

Observasi	Ranking
Observasi	X	Y
D	1	2
C	2	4
A	3	3
B	4	1

Untuk mencari S, maka lihat ranking Y. Dari pembahasan tersebut ditemukan S = -2, sedangkan N = 4. Jadi, korelasi Kendall Tau yang didapatkan menjadi:

Dari contoh perhitungan sederhana diatas, didapat nilai korelasi Kendall Tau adalah 0,33.

z = x - μ z σ x = x - N P N P Q - - - - - \sqrt

τ = - 2 1 2 4 ( 4 - 1 ) = 0, 33

KORELASI SPEARMAN

Koefisien korelasi Spearman atau sering disebut juga sebagai Spearman Rank Correlation Coefficient, digunakan untuk menghitung korelasi berdasarkan data yang berbentuk peringkat (ranking).

Jika dilakukan secara manual, maka tata tertib melakukan uji korelasi Spearman adalah:

Jumlahkan skor item-item di tiap variabel untuk mendapatkan skor total variabel (misalnya cari skor total variabel X dengan menotalkan item-item variabel X).
Lakukan rangkin skor total x (rx) dan rangking skor total y (ry).
Cari nilai d yaitu selisih rx – ry .
Cari nilai d2 yaitu kuadrat d (selisih rx – ry).

Perhitungan koefisien korelasi Spearman, yaitu:

Apabila tidak terdapat peringkat yang “kembar/sama” (“tied rank”). Rumus yang digunakan untuk menghitung korelasi Spearman tanpa peringka sama adalah

Apabila terdapat peringkat yang “kembar/sama” (“tied rank”). Rumus yang digunakan jika terdapat ranking kembar yaitu

Keterangan:

Contoh Soal

Sebuah perusahaan sedang melakukan rekrutmen pegawai. Pimpinan perusahaan ingin mengetahui apakah ada hubungan antara nilai ujian tertulis dengan jumlah barang yang dijual oleh masing-masing salesman yang baru direkrut tersebut. Di bawah ini adalah data mengenai ranking nilai ujian tertulis dan ranking hasil penjualan dari sampel 10 orang salesman yang baru direkrut.

Salesman	Ranking Nilai Ujian Tertulis	Ranking Jumlah Penjualan
A	5	3
B	6	7
C	8	5
D	3	1
E	2	6
F	7	8
G	1	2
H	4	9
I	10	4
J	9	10

Jawaban :

Hipotesis

H0: Tidak ada hubungan antara ranking nilai ujian tertulis salesman dengan rangking jumlah penjualan oleh salesman di tingkat populasi

H1: Ada hubungan antara ranking nilai ujian tertulis salesman dengan rangking jumlah penjualan oleh salesman di tingkat populasi

Tingkat Signifikansi

$α = 5 %$

Statistik uji

Data yang sudah di ranking.

Salesman	Ranking Nilai Ujian Tertulis	Ranking Jumlah Penjualan	$d_{i}$	$d_{i}^{2}$
A	5	3	2	4
B	6	7	-1	1
C	8	5	3	9
D	3	1	2	4
E	2	6	-4	16
F	7	8	-1	1
G	1	2	-1	1
H	4	9	-5	25
I	10	4	6	36
J	9	10	-1	1
				$\sum = 98$

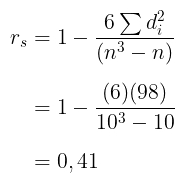
Kemudian, dari tabel korelasi Spearman diperoleh nilai $r_{s} (0, 05; 10) = 0, 648$ .

Karena $r_{s}$ hit < $r_{s}$ tabel (0,41 < 0,648) maka diputuskan gagal tolak H0.

Dengan tingkat signifikansi 5% belum cukup bukti untuk mengatakan terdapat hubungan/keterkaitan ranking nilai ujian tertulis dengan ranking jumlah penjualan.

Cari Blog Ini

Ria Suci